界面張力梯度驅動對流是空間自然對流熱質輸運的基本形式，對其時空轉捩過程、轉捩機制、非線性特征及流動向湍流轉捩途徑等基本規律的研究，一方面可以豐富非線性動力學的相關理論，另一方面對于人類認識、探索和利用空間環境也具有重要的應用價值，是微重力流體物理的重要研究內容和學科前沿。本文對目前的研究現狀進行了總結，重點介紹了研究液層界面張力梯度驅動對流的實驗及數值模擬方法，雖然已有的研究已經得到在不同模型和工況下的各種轉捩模式，但是在轉捩規律上仍需要更深入的探索，可以從以下幾個方面著手：

（1）理論分析和數值模擬結果的正確性需要由實驗來驗證，空間實驗可以滿足微重力環境、長時間觀測的要求，但是空間實驗有一定難度且機會來之不易，故而可以考慮進一步發展實驗手段，以實現數值模擬中采用的更豐富的工況；以及加強對實驗條件的控制，以降低無關因素的干擾，提高實驗精度。

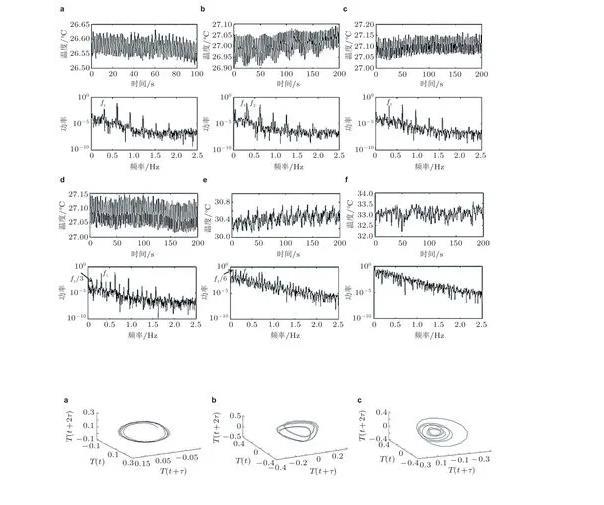
（2）目前關于液層界面張力梯度驅動對流向湍流的超臨界轉捩在數值方法上主要有流動時序數據的分析和分岔問題的數值算法。流動宏觀量的時序數據來自實驗結果或者直接數值模擬，對于后者，需要對于不同參數分別進行數值模擬，再通過時間序列頻譜及其混沌特性的定量計算分析流動轉捩規律，即在大量的離散的數據序列中尋找分岔點，故此過程比較繁瑣。而通過構造分岔方程對分岔進行數值計算的方法雖然可以一步到位，但是在選取分岔方程，解高維線性、非線性方程等過程中均需要根據具體的流動模型進行調整，具有一定難度，且對于更加復雜的流動模式需要更大的計算量，用此算法也無法直接計算得到混沌解。上述兩種方法各有優缺點，目前在轉捩過程的數值研究中較為常用的仍是在不同參數下進行直接數值模擬，而后對大量數據進行頻譜分析，識別分岔點；在直接對分岔進行數值計算的研究中，也常常需要通過直接數值模擬來驗證分岔得到的解的可靠性與準確性，在今后的研究中可考慮進一步將兩種方法結合運用，互相補充、驗證。

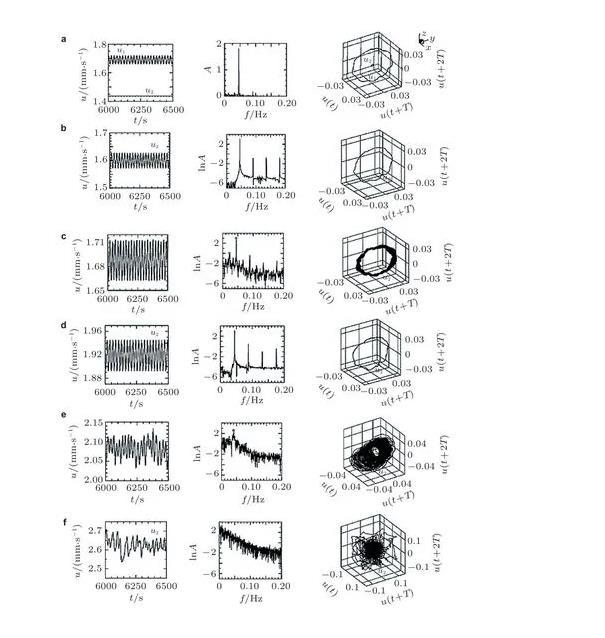
（3）液層界面張力梯度驅動對流向湍流轉捩的過程中會產生豐富的流動模式，轉捩過程除了與上文提到的液層模型、無量綱參數（Prandtl數、高徑比、體積比等）有關，還受到熱邊界條件（如體系是否絕熱）、加熱方式及加熱速率等因素的影響；此外，在具體的應用場景中通常有多種流動相互作用，考慮界面張力梯度驅動對流與其他諸如浮力、電磁場、旋轉等效應的耦合，對于重新檢視已發現的轉捩途徑以及尋找新的轉捩途徑均有一定的積極意義。

（4）目前對于液層界面張力梯度驅動對流向湍流轉捩的研究仍不夠完善，在對超臨界轉捩階段的實驗及數值模擬研究中觀察到了許多復雜的轉捩模式，但大多只是現象上的描述，并未總結出普遍的規律；對于流動最終能否通向混沌暫無普適的判據，流動通向混沌過程中出現的諸如陣發、鎖頻等特殊的現象也尚未有更本質的機理上的解釋?？傊瑢τ谵D捩規律的深入理解，需要界面張力梯度驅動對流這一非線性模型在理論上的進一步發展，未來道阻且長。