合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 水、常溫液態金屬等9種流體對液滴碰撞壁面影響的數值研究(三)
> 水、常溫液態金屬等9種流體對液滴碰撞壁面影響的數值研究(二)
> 水、常溫液態金屬等9種流體對液滴碰撞壁面影響的數值研究(一)
> 彈簧秤測量水的表面張力系數實驗裝置改進措施及效果
> 電暈對BOPP薄膜表面張力、化學結構、元素組成的影響
> 半泡法測定液體表面張力系數理論、實驗設計
> 全氟庚烷端基聚丙烯酸(FPAA)合成方法及水溶液表面張力測定
> 純聚苯胺LB膜和聚苯胺與乙酸混合的LB膜制備、NO?氣體敏感特性研究(下)
> 純聚苯胺LB膜和聚苯胺與乙酸混合的LB膜制備、NO?氣體敏感特性研究(上)
> 不同相對兩親面積的Janus顆粒在油氣表面性質和泡沫性能對比(三)
水、常溫液態金屬等9種流體對液滴碰撞壁面影響的數值研究(一)
來源:《清華大學學報(自然科學版)》 瀏覽 11 次 發布時間:2025-09-16
摘要:不同學者對液滴碰撞動力學的研究結論具有差異,研究的流體種類也較為單一。該文建立的研究體系包含了水、甘油水溶液、硅油、常溫液態金屬在內的9組流體,將流體黏度、表面張力的研究范圍擴展至1——970 mPa·s、20——500 mN/m,通過相場法數值模擬,補充低Reynolds數Re的液滴碰撞數據,探索已有理論的適用性。研究表明:碰撞初期,鋪展因子β隨無量綱時間τ變化的已有理論主要適用于Re>100的情況。最大鋪展因子βmax與Weber數We在毛細力區滿足βmax∝Web,在黏性力區滿足βmax∝Reb,與已有理論相符,壁面潤濕性對指數b的影響具有規律。最小中心厚度hmin僅在We≥10時與已有理論hmin∝Re-0.5相符;We<10時,hmin受到壁面潤濕性和表面張力的明顯影響。而當Re趨近于1時,βmax和hmin*由液滴初始動能和壁面潤濕性決定,偏離上述冪函數規律。
液滴碰撞壁面是常見的兩相流現象,廣泛存在于應急噴淋冷卻、汽水分離再熱、電路印刷等各種工業科技領域。液滴在壁面上的運動行為對許多物理過程有重要影響,例如在噴淋冷卻中,需要增大液滴碰壁后的鋪展直徑D,并減小液滴中心厚度hc,從而擴大換熱面積,促進流體蒸發,利用汽化潛熱加強散熱。液滴碰撞壁面后的運動狀態,主要受流體性質、壁面潤濕性、碰撞速度、入射角度等因素的影響。通過研究上述因素與液滴行為的內在聯系,有效控制液滴運動,揭示其動力學機理,是研究和應用的共同需要。在近20年里,隨著高速攝像技術的應用和普及,液滴碰撞動力學得到了快速發展。
為描述初始直徑D0的液滴以速度U0垂直碰撞壁面后的形態變化,研究者們用鋪展因子β=D/D0表征液滴直徑變化,用無量綱中心厚度h=hc/D0表征液滴厚度變化,觀測β和h隨無量綱時間τ=t·U0/D0變化的情況,重點關注最大鋪展因子βmax和最小中心厚度hmin*.針對上述參數,學者們開展了大量研究。
根據β隨τ變化情況,液滴碰撞分為運動、鋪展、弛豫和平衡4個階段,如圖1所示。在運動階段(τ<0.1),慣性力占主導地位,液滴上部仍保持球狀,下部鋪展成楔形邊緣,文指出該階段可忽略流體性質影響,β隨τ呈指數上升,即β∝τb,其中指數b介于0.45到0.57之間,一般取b=0.5;在鋪展階段,受黏性力或毛細力的主導作用,β逐漸增至βmax,然后液滴開始回撤收縮,進入馳豫階段;在平衡階段,液滴可能穩定鋪展,也可能發生反彈,或者碎裂飛濺。本文主要針對運動階段和鋪展階段進行研究。
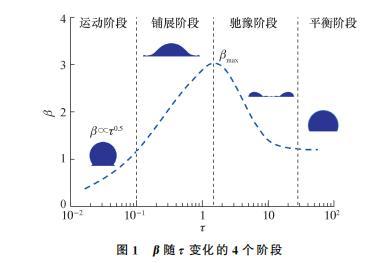
圖1β隨τ變化的4個階段
對于直徑小于其毛細長度的液滴碰撞(即ρgD02<σ,其中ρ和σ分別是液滴的密度和表面張力,g為重力加速度;本文研究體系均滿足該條件),一般認為βmax主要受We和Re這2個特征數控制。We=ρD0U02/σ,Re=ρD0U0/μ,其中μ是液滴的黏度。
1996年,Pasandideh-Fard等對水滴碰撞進行實驗和數值研究,認為βmax由We、Re和前進接觸角θa共同決定:βmax=[(We+12)/(3-3cosθa+4We/Re0.5)】0.5.2009年,Roisman等通過理論推導,認為在We、Re較大的情況下,有βmax=0.87Re0.2-0.40Re0.4We-0.5.上述預測模型認為We和Re都對βmax產生影響,而Bartolo等、Clanet等、Eggers等利用碰撞因子P=We/Reb(0<b<1)判定液滴鋪展由哪種力主導,認為當毛細力主導鋪展時,βmax由We決定;當黏性力主導鋪展時,βmax由Re決定。
h隨τ變化分3個階段:降低階段、平臺階段、回升階段。在降低階段的初期,受慣性力主導,h隨τ線性降低。當U0較大時,hmin接近黏性邊界層厚度,h保持在hmin一段時間即進入平臺階段。隨后,受表面張力作用,h進入回升階段。
對于hmin,2010年Schroll等數值模擬了硅油碰撞平面,忽略空氣影響,發現hmin由邊界層厚度決定。2010年,Eggers等通過數值模擬,認為當Re較大時存在規律hmin∝Re-0.4,但對于Re較小的情況,可以忽略雙曲流影響,有hmin∝Re-0.5.2012年,Lagubeau等通過實驗測量水和甘油溶液液滴碰撞平面,認為在100<Re<10000的范圍內,hmin*與Re-0.4成正比。2017年,Zhu等通過數值模擬液滴撞擊球面,認為當We較小時,表面張力也顯著影響液滴厚度。
βmax和hmin*的多種預測模型如表1所示。從表1可以看出,在黏性力區,已有的理論、實驗和模擬研究普遍認為βmax主要由Re控制,與Re0.2成正比,但目前實驗數據和模擬驗證均較少,已有實驗主要針對硅油、甘油溶液,黏度在300 mPa·s以內,缺乏對于更高黏度液體的研究;另外,Eggers等的模擬研究不針對真實流體,且忽略空氣影響和假設壁面完全疏水,與現實情況具有差異。在毛細力區,盡管Eggers等的模擬結果與Fedorchenko等的理論相符合,都認為βmax∝We0.5,但Clanet等的實驗結果卻表明βmax∝We0.25,實驗所得We指數大小僅為理論的一半。因此,仍需對βmax進行更多的實驗、模擬研究。
針對hmin的實驗和模擬研究結論主要基于水和甘油溶液,研究流體種類較少;同時,Lagubeau等的實驗結論hmin∝Re-0.4和Du等的數值結果hmin∝Re-0.5也存在一定差異,盡管2種結論所基于的Re范圍有所不同,但Re是否對指數有直接影響以及Re是否為hmin的唯一影響因素,有待進一步探討。
綜上所述,針對βmax和hmin*的研究,不同學者所得結論具有差異,研究的流體種類也較為單一,We和Re的研究范圍也各不相同。因此本文采用相場法,對9組真實流體碰撞不同潤濕性平面進行數值模擬,將μ和σ的研究范圍分別擴展為1——970 mPa·s和20——500 mN/m,并通過改變U0,獲得1≤Re≤18600、1≤We≤4660的測試體系,探索流體性質、壁面潤濕性等因素在液滴碰撞過程中的作用機理,補充了低Re液滴碰撞數據,探索已有理論的適用性,嘗試揭示更具普適性的液滴碰撞機制。
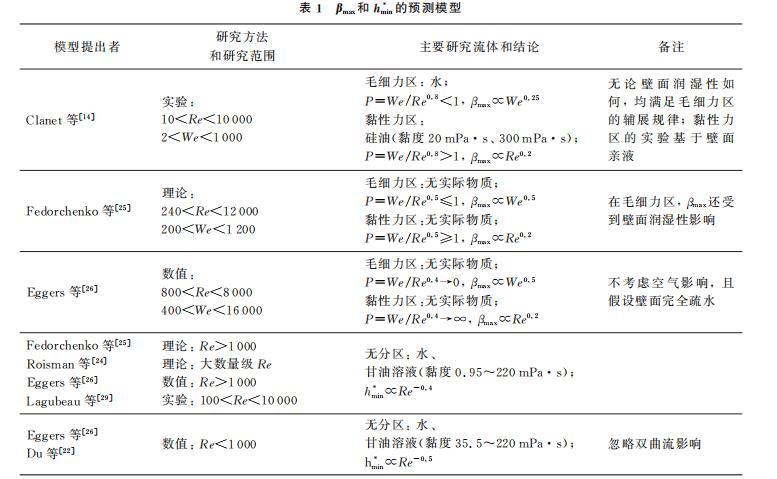
表1βmax和hmin*的預測模型










